开篇

虽然数据挖掘算法很多，但有过实际经验的同学肯定都知道，集成方法(ensembel method)大多数情况下都是首选。集成方法和LR、SVM算法不同，她不是一个具体的模型或算法，而是一类算法的统称。集成，从其字面意思也能看出，这家伙不是单兵作战，而是依靠团队取胜。简而言之，集成方法就是通过构建并结合多个学习器来完成学习任务。这句话有两个地方需要注意，“如何构建每一个学习器”以及“如何结合多个学习器而产生预测结果”。

如果我们按照“如何构建每一个学习器”来将集成方法分类，总体可以分为两类：1) 个体学习器减存在强依赖关系、必须串行生成的序列化方法，代表方法是Boosting；2）个体学习器之间不存在强依赖关系、可同时生成的并行化方法，代表方法是Bagging。

本文要讲到的Gradient Boosting就属于Boosting方法。

由于Gradient Boosting涉及到的知识实在是很多，完全可以写成类似"Understanding Random Forest: From Theory to Practice"的博士论文，由于水平和时间的限制，本文不会涉及过多、过深的细节，而是尽量用通俗的自然语言和数学语言来解释我对Gradient Boosting的浅显理解，仅仅是入门水平:)

决策树

既然要讲Gradient Boosting，那么决策树肯定是绕不开的，虽然Boosting方法对"个体学习器"没有要求，你可以选择LR、SVM、决策树等等。但是大多数情况下我们默认都选择决策树作为个体学习器。下面简单解释决策树算法。

决策树，顾名思义，根据树结构来进行决策。这种思想是很质朴的，和我们人类做决策时的思考过程很像，比如明天出门要不要带伞啊？如果我根据天气情况来做出决定，可以记作：

if 明天下雨：
    出门带伞
else:
    出门不带伞

看到没有，决策过程可以用if, else来具体化，难怪有人说，决策树就是一堆if else而已。数据挖掘比赛中很多人会首先用简单的规则跑出一个结果，这实际上就是在人工构造决策树啊。

既然决策树是一种机器学习方法，我们就想知道她的学习过程是怎么样的，也就是给定训练集如果构建一颗决策树呢？通常，决策树的构建是一个递归过程:

1 输入训练集D，特征集F
2 如果D中样本全属于同一个类别C，将当前节点标记为C类叶节点，返回
3 从F中选择最优划分特征f
4 对于f的每一个值\(f_i\), 都生成一个子节点，然后对D进行划分，f值相同的样本都放到同一个子节点，并对节点进行标记，然后对于每一个新产生的子节点，进行第1步

注意：实际上对于决策树，大多数的实现方法都是基于二叉树，比如sklearn。

划分选择

决策树算法的关键是上面的第3步，即如何选择最优划分特征。如何评价一个特征是不是优秀呢？基本的原则就是看按照某一个特征生成子节点后，子节点的样本是不是都尽可能属于同一个类别，也就是子节点的纯度越高，我们就认为这个特征"好"。

为了量化子节点的纯度，前人提出了很多具体的评价方法，包括信息增益、信息增益率和基尼指数。这些评价方法大同小异，我们就以最常见的信息增益(Information Gain)为例进行解释：

假设当前节点包含的数据集为D，则数据集的熵(entropy)定义为：

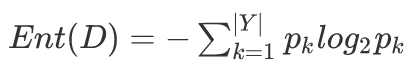
其中\(|Y|\)表示类别值的取值个数。

假设某一个特征\(f\)有V个可能的取值 \(f^{1},f^{2},…,f^{V}\), 若使用特征\(f\)对\(D\)进行划分，会产生\(V\)个子节点，其中第\(v\)个子节点包含了\(D\)中所有\(f\)取值为\(f^{v}\), 记作\(D^{v}\). 按照下式计算用\(f\)对\(D\)进行划分获得的信息增益(information gain):

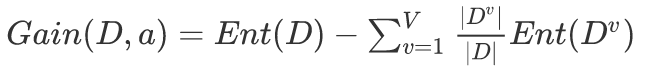
信息增益越大，我们就认为用\(f\)划分所获得的纯度提升越大。

下面是用信息增益来构建决策树的简单Python代码，注意，构建的是二叉树。

def uniqueCounts(X):
    """
    对y的取值进行计数, 用于计算节点的purity
    rvalue: 计数结果
    """
    results = {}
    for row in X:
        y = X[-1]
        results[y] = results.get(y, 0) + 1
    return results


def entropy(X):
    """计算熵"""
    from math import log
    log2 = lambda x: log(x)/log(2)
    results = uniqueCounts(X)

    entropy = 0.0
    for y in results:
        p = float(results[y])/len(X)
        entropy = entropy - p*log2(p)
    return entropy


# 定义节点
class DecisionTreeNode:
    def __init__(self, col=-1, value=None, results=None, tb=None, fb=None):
        self.col = col #
        self.value = value
        self.resuls = results
        self.tb = tb
        self.fb = fb


import numbers
def divideSet(X, column, value):
    """
    用某个特征对数据集进行分割, 分为两个数据集，二叉树
    """
    split_function = None
    if isinstance(value, (numbers.Integral, np.int)) or isinstance(value, (numbers.Real, np.float)):
        split_function = lambda row: row[column] >= value
    else:
        split_function = lambda row: row[column] == value

    # 将数据集分为两个集合，并返回
    set1 = [row for row in X if split_function(row)]
    set2 = [row for row in X if not split_function(row)]
    return (set1, set2)


def buildTree(X, scoref=entropy):
    """
    以递归方式构建树， 使用信息增益
    """
    if len(X)==0:
        return DecisionTreeNode()

    current_score = scoref(X)
    # 记录最佳拆分属性, 以及用哪个属性值
    best_gain = 0.0
    best_criteria = None # 拆分用的属性和属性取值
    best_sets = None # 拆分后的两个数据子集

    feature_nums = X.shape[1] - 1
    # 遍历每一个特征以及每个特征的每一个取值来构建树，复杂度很高, 可以用特征的中位数
    for col in range(feature_nums):
    # 在当前列中生成一个由不同值构成的序列
        column_values = {} #记录数据集中第col个特征，每个不同取值的个数
        for row in X:
            column_values[row[col]] = 1 # 初始化

        # 根据当前列的特征每个取值， 尝试对数据集进行分割
        for value in column_values:
            set1, set2 = divideSet(X, col, value)

            # 信息增益
            p = float(len(set1)) / len(X)
            gain = current_score - p*scoref(set1) - (1-p)*scoref(set2)
            if gain > best_gain and len(set1) >0 and len(set2) >0 :
                best_gain = gain
                best_criteria = (col, value)
                best_sets = (set1, set2)

    # 创建子分支
    if best_gain > 0:
        trueBranch = buildTree(best_sets[0])
        falseBranch = buildTree(best_sets[1])
        return DecisionTreeNode(col=best_criteria[0], value=best_criteria[1],
                                    tb = trueBranch, fb=falseBranch)
    else:
        return DecisionTreeNode(results=uniqueCounts(X))

Gradient Boosting

经常参加数据挖掘比赛(Kaggle、天池)的同学肯定对XGBoost、GBDT如雷贯耳，特别是XGBoost，简直堪称DM居家必备之神器。马克思老人家说过，透过现象看本质。XGBoost之所以这么吊，除了牛叉的代码实现，也和她的算法原理, Gradient Boosting, 有直接联系。下面我们就开启Gradient Boosting入门之旅吧。

Gradient Boosting, 又被称为Gradient Boosting Decision Tree(GBDT)、Gradient Boosting Machines(GBMs) 或者 Gradient Boosted Trees(GBT), 虽然别名很多，但只要看到gradient和boost这两个词，就能确定指的就是本文的Gradient Boosting.

Gradient Boosting除了名字多以外，她的应用范围也很广，可直接应用于分类(Classification)、回归(Regression)和排序(Ranking)。

残差和梯度

和其他Boosting算法一样，Gradient Boosting可以记作：

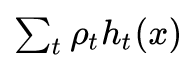
这个式子很好理解，\(h_{t}(x)\)是个体学习器，Gradient Boosting就是把每一个个体学习器集成到一起。

前面我们提到Boosting通过串行的方式构建个体学习器，换句话说，个体学习器是按照顺序一个个构建的，比如迭代式或者递归的方式。而每一个学习器当然也不是随意创建的，比如AdaBoost每一个学习器都会重点关注上一个学习器分类错误的那些样本点，通过为每个样本赋予不同的权重实现。

我们先不讲Gradient Boosting背后的原理，单就看他的名字，我当初就很疑惑，gradient? 模型集成和梯度有半毛钱关系啊？更别提GBDT里面不但有gradient还有tree，梯度和决策树是怎么搞到一起的？

带着这些疑问，让我们一步步揭开Gradient Boosting的面纱。

首先，来思考一个回归问题：现有训练集D={\(x_i,y_i\)}和一个已经在D上训练好的模型\(F\), 不过\(F\)在D上的表现不太好，你能否按照如下规则来得到一个令人满意的模型：

不能对\(F\)做改动
你可以利用D单独训练决策树模型h，但是必须用F(x)+h(x)作为最终的模型

我们希望最后的模型F+h效果如下：

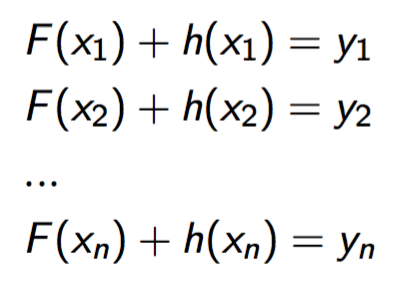
上面的等式等价为：

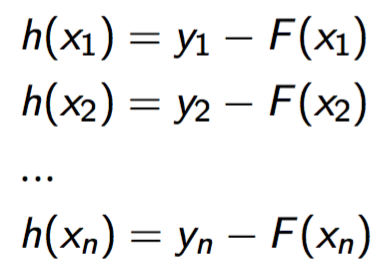
看到这里你会发现，对于决策树h，她的训练集实际上是{\(x_i\), \(y_i-F(x_i)\)}！而y-F(x)在数学界是有名号的，被称作残差(residual)。我们再回过头来看h的物理意义，她的作用其实是修正F的错误，也就是抵消F的误差。

如果F+h在D上的表现还是令人不太满意。

我们不断构建决策树，最终会得到一个强大的模型F+\(\sum h_{t}\), 这实际上就是Gradient Boosting的学习过程。

看到这里你肯定会疑惑，这明明是 Residual Boosting！和梯度有毛线关系啊？且看下面的推导：

假设我们要训练模型F(x), 损失函数选用平方差损失函数,

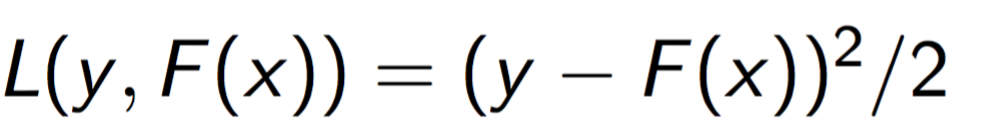
我们想要最小化:

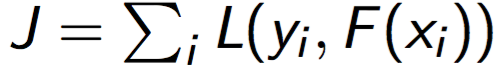
由于F(\(x_{i}\))也是一个实数，我们不妨把F(\(x_{i}\))当做L的参数，如果用梯度下降算法来优化L,

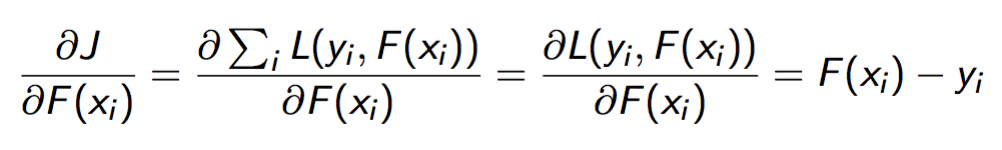
仔细看梯度，竟然和残差有直接的联系：

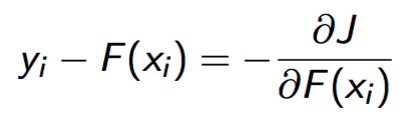
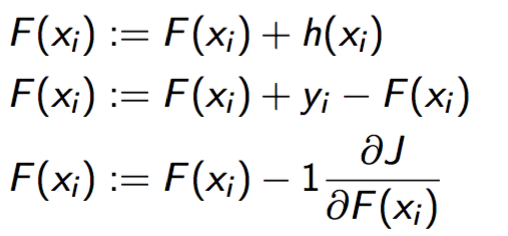
现在，我们可以用梯度下降的思想来解释损失函数为平方差时，Gradient Boosting的学习过程：

1 构建初始学习器F, 比如\(y_{i}\)的平均值
2 计算平方差损失函数的梯度g
3 用(x,-g) 训练决策树h
4 F = F + 1*h
5 如果决策树个数达到阈值，结束；否则，跳转到第2步

Gradient Boosting可不是仅能用平方差损失函数哦，以sklearn为例，用于回归的GradientBoostingRegressor支持least square loss、least absolute loss、hubor loss和quantile loss；用于分类的GradientBoostingClassificier支持logistic regression和exponential loss。

我们可以把梯度看做残差的泛化形式，则任何函数都可以作为Gradient Boosting的损失函数！只要你能提供她的梯度！这也是XGBoost支持自定义损失函数的原理基础。

所以，Gradient Boosting的学习过程：

1 构建初始学习器F, 比如\(y_{i}\)的平均值
2 计算损失函数的梯度g
3 用(x,-g) 训练决策树h
4 F = F + \(\rho\) h, \(\rho\)为学习率
5 如果决策树个数达到阈值，结束；否则，跳转到第2步

过拟合与正则化

随着Gradient Boosting中决策树个数的增加，通常你会发现在训练集D上的效果越来越好，如果是二分类问题，甚至可能准确率接近100%，此时就要注意了，很可能产生了过拟合(overfitting)现象。任何一个能实际应用的模型，都必然会考虑到过拟合现象，我们来看一下Gradient Boosting如何减弱过拟合。

子采样(subsampling)

一个模型如果在训练集上表现很好，在测试集上表现远不如训练集，我们就认为这个模型陷入了过拟合。她把训练集中存在的噪声错误地归类为数据的普遍性规律，怎么样降低噪声对模型的干扰呢？如果我们把噪声看做数据集中的异常点，在训练模型的时候，我们引入随机性因素，比如从训练集中随机抽取样本来训练模型，无疑会减弱异常点的干扰。这就是子采样的思想。

在每一次构建新的决策树之前，先从训练集中随机抽取部分样本构建一个新的训练集\(D_t\)，然后利用\(D_t\)训练决策树。

sklearn的GradientBoostingRegressor和GradientBoostingClassifier提供了subsample参数进行子采样。

收缩(shrinkage)

Shrinkage也是常用的减弱过拟合的手段之一，在Gradient Boosting中，shrinkage用于降低每一个个体学习器的影响，在sklearn中，shrinkage就是我们通常见到的学习率, 即，GradientBoostingRegressor和GradientBoostingClassifier中的learning_rate参数。

这里多说一句，原始的Gradient Boosting算法在每一次学习到个体学习器后，还要学习一个参数叫做步长(step length)的参数，步长和shrinkage是两个参数，不要搞混，但是在sklearn的实现中，并没有考虑步长，直接用学习率代替了shrinkage.

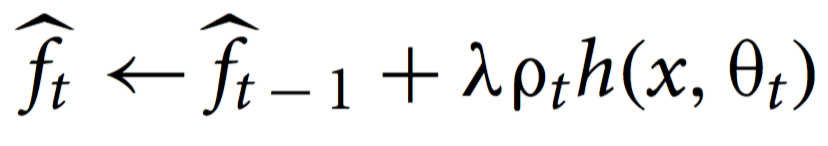
用来减弱过拟合的方法有很多，比如还有early stopping, GradientBoostingRegressor和GradientBoostingClassifier还提供了\(monitor\)参数, 可以用于early stopping。

XGBoost

Gradient Boosting的开源实现有很多，但目前最流行最好用的肯定是XGBoost。 XGBoost之所以这么好用，一部分原因是陈天奇等人强大的编码能力和优秀的系统设计，另一方面也是因为她对传统Gradient Boosting在算法层面做出了诸多改进。本文不涉及并行化和系统设计的内容，我仅谈一下XGBoost在算法层面的改进之处。

带有正则项的目标函数

大部分机器学习算法的学习过程可以转换成一个优化问题，目标函数=损失函数＋正则项。而传统的Gradient Boosting是不包含正则项的，所以，XGBoost做出的第一项改进就是修改目标函数，增加如下的正则项：

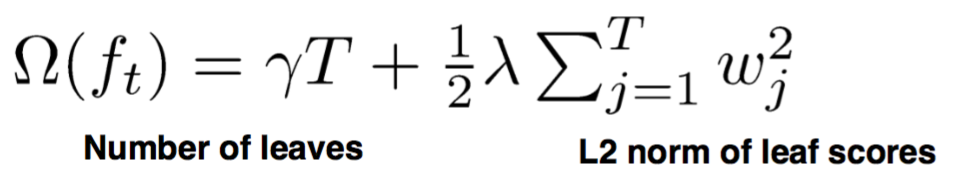
这个正则项量化了每一颗CART树的复杂度，其中T是CART树\(f_t\)的叶子节点数目，\(w\)是叶子节点的权重。看一个简单的例子：

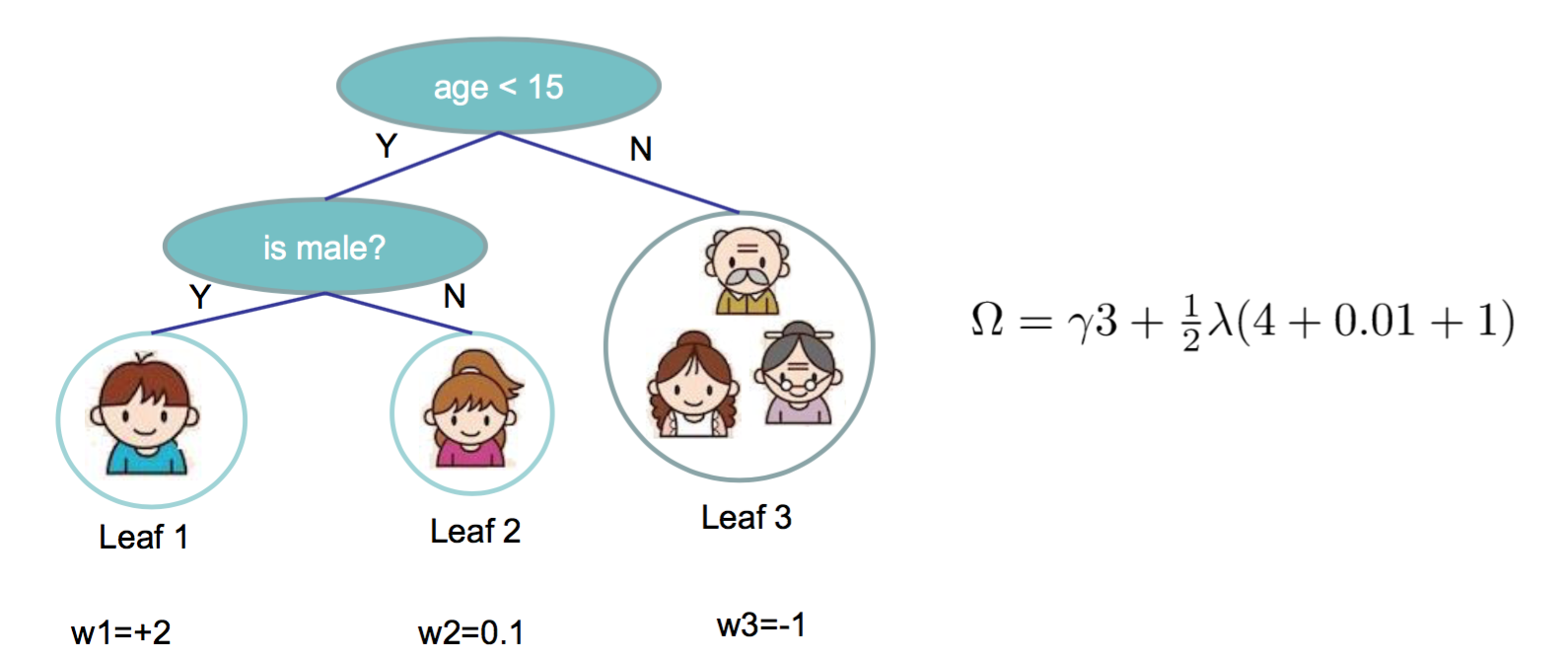
目标函数的近似

XGBoost在对目标函数进行优化求解时，采用了近似手段，

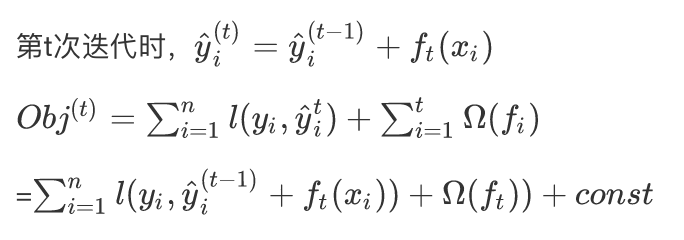
然后对损失函数泰勒展开：

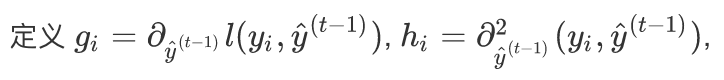
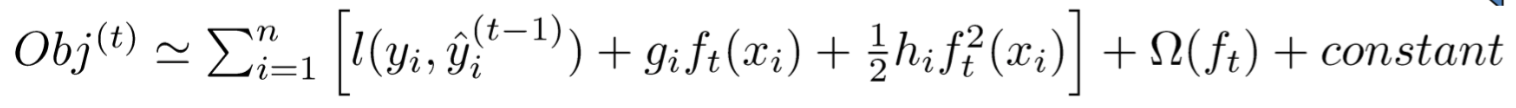
进一步移除目标函数中的常量，

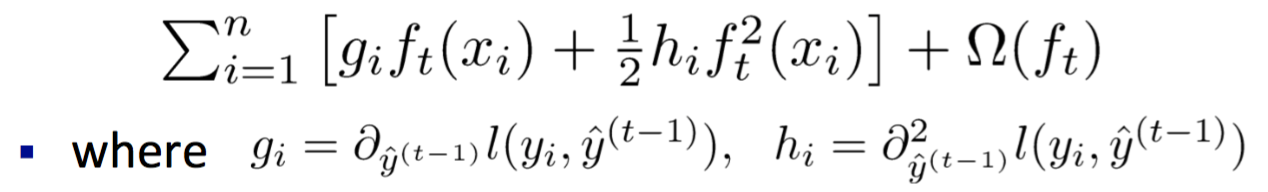
上面的\(f_{t}(x)\)表示一颗决策树，我们能否只用叶子节点表示一棵树呢？答案是可以，但需要知道两方面的知识，一是叶子节点的权重\(w\), 二是每个叶子节点的样本点(即，树的结构)，用p表示。

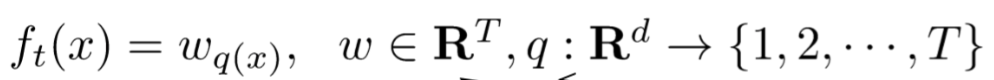
进一步我们按照样本点在CART树种的分布情况，可以将训练集样本分为T组，得到：

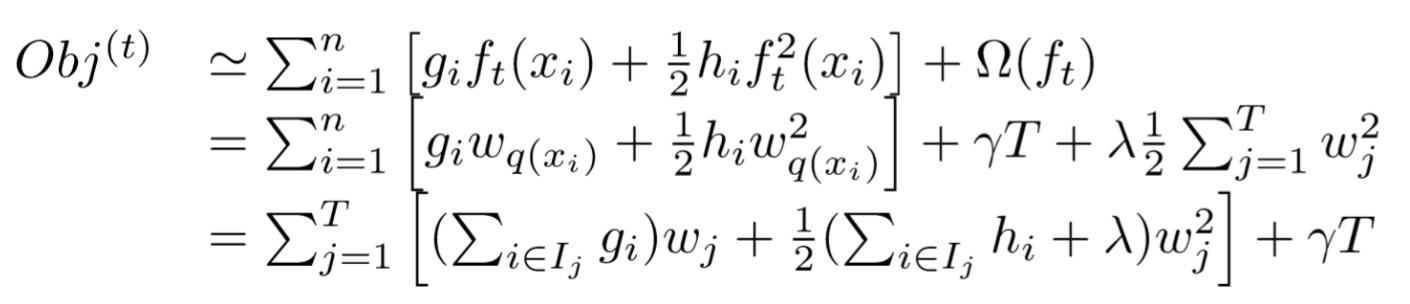
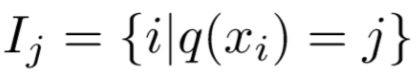
上式其实是T个二次函数的和，我们知道对于单变量二次函数\(ax^2+bx\)，当x取值为\(-b/(2a)\)时，函数有极值\(-b^2/(4a)\),

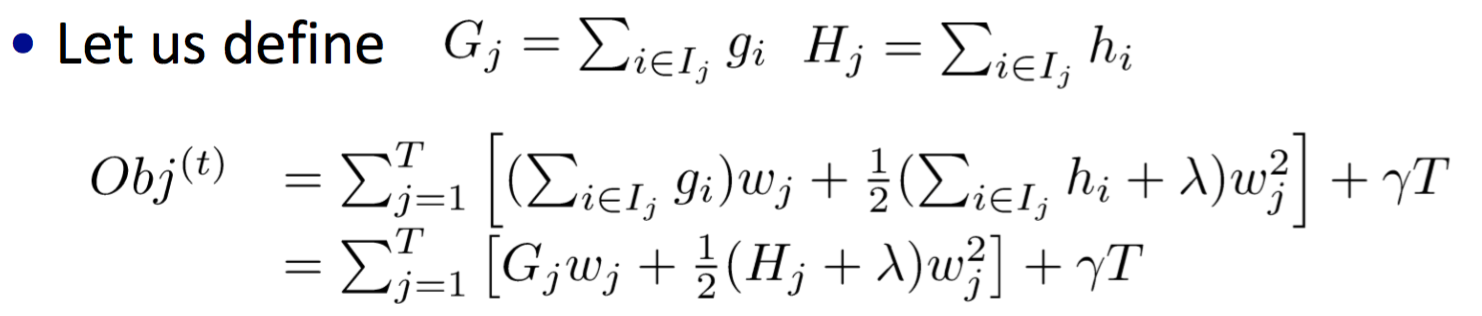
我们可以得到每个叶子节点对应的\(w\)的最佳取值和函数极值:

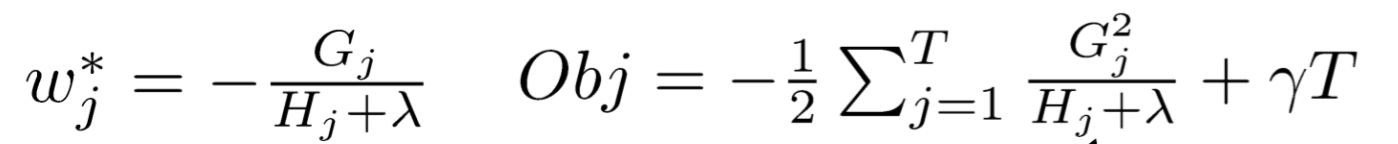
看一个具体的例子：

近似贪心算法

决策树分割节点时，一般使用贪心算法，并且需要遍历所有特征以及特征的每一个取值，这种做法称为精确贪心算法(exact greedy algorithm), XGBoost和sklearn一样支持这种精确贪心算法，除此之外，XGBoost还包含了陈天奇等人提出的决策树分割节点的近似算法和针对稀疏数据的分割节点快速算法。对于近似算法，我说一下自己的错误理解:

不论精确还是近似算法，都需要遍历一遍特征，近似算法的有点是不需要遍历特征的每个取值，她只遍历特征取值范围的百分位数上那些取值，那么如何取得这些百分位数值呢？可以用quantile sketch算法，事情到这里是不是就结束了呢？No，陈提到quantile sketch算法没有考虑到样本权重问题，如果数据集中的数据点是有权重的，这个算法就不适用了。于是陈等人提出了一种可以使用于带权重数据的quantile sketch算法。

其他优点

前面说过，理论上Gradient Boosting的损失函数可以是任意可微函数。只要能够提供损失函数的梯度和Hessian矩阵，用户就可以自定义训练模型时的损失函数。 XGBoost也允许用户在交叉验证时自定义误差衡量标准。也可以选择使用线性模型替代树模型，从而得到带L1+L2惩罚的线性回归或者logistic回归。

开篇#

决策树#

划分选择#

Gradient Boosting#

残差和梯度#

过拟合与正则化#

子采样(subsampling)#

收缩(shrinkage)#

XGBoost#

带有正则项的目标函数#

目标函数的近似#

近似贪心算法#

其他优点#

开篇

决策树